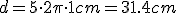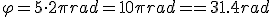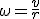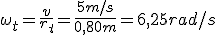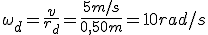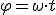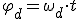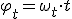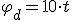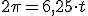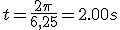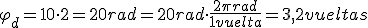1.5 Magnitudes lineales y angulares

1.6 Movimiento circular uniforme: periodo y frecuencia

Hay un caso de mcu que tiene un interés especial: se trata de aquellos mecanismos en los que el mcu se transforma en movimiento lineal. Es decir, auitomóviles, tractores, bicicletas, etcétera, en los que el giro de las ruedas apoyadas sobre el suelo hace que el móvil avance a retroceda.

¿Cómo podemos determinar la velocidad lineal del móvil si sabemos la velocidad angular de sus ruedas? ¿Y el espacio recorrido a partir del ángulo girado? Para ello, es necesario establecer la relación existente entre magnitudes lineales y angulares.

Caso de estudio

Fotografía de Jester79 bajo licencia GNU

Vas a comprobar de forma experimental la relación entre ángulo girado y espacio recorrido. Para ello, deberás utilizar un coche o tractor de juguete, que tenga unas ruedas de al menos 2 cm de diámetro. Haz una marca blanca en el lateral de la rueda (usa corrector typex o algo parecido). Apoya la rueda de forma que el punto marcado quede junto al suelo, y haz una marca con lápiz en ese punto de apoyo. Mueve el coche de forma que la rueda gire cinco vueltas completas, contando una cada vez que el punto marcado quede junto al suelo, y haz otra marca en el suelo al finalizar el recorrido.

Mide la distancia entre las dos marcas, que corresponderá al espacio recorrido en cinco vueltas de rueda. Mide ahora el diámetro de la rueda, con lo que sabrás su radio. Utiliza un flexómetro o una regla.

Ahora, calcula el valor de cinco veces la longitud de la circunferencia (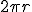) y compáralo con el espacio medido sobre el suelo. ¡El resultado debe ser aproximadamente el mismo!

Por último, solamente debes tener en cuenta que cuando la rueda da un giro completo, ha descrito un ángulo de 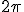radianes, y ha avanzado 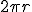metros. Es decir, el espacio recorrido es el ángulo descrito en radianes multiplicado por el radio.

Una partícula cuando se mueve sobre una circunferencia describe un ángulo 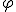pero también recorre un espacio sobre su trayectoria. ¿Existe alguna relación entre ambas magnitudes? Sí y es muy sencilla de obtener. Vayamos a un caso particular. Imagina que el móvil ha dado una vuelta completa. El espacio que habrá recorrido es justo la longitud de la circunferencia, es decir:

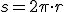
Como vemos el espacio es el producto del ángulo completo por el radio. Si en vez de haber dado una vuelta completa, hubiera dado media entonces el espacio recorrido sería:

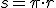
De nuevo el producto del ángulo correspondiente a media circunferencia por el radio. En el caso de que se haya batido un ángulo 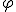cualquiera, el espacio recorrido será:

Esta misma relación se da entre las velocidades y las aceleración tangencial:

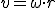
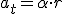
En el caso de la aceleración normal la relación es:

Actividad

Las magnitudes lineales s, v y a_t se pueden calcular multiplicando las angulares por el radio de giro, con todas las unidades en el Sistema Internacional.

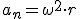
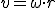
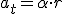
A continuación te mostramos un resumen las ecuaciones de los diferentes movimientos que hemos estudiado hasta ahora así como las de los MCU y del movimiento circular uniformemente variado. Podrás observar que son muy similares.

Movimiento rectilíneo y uniforme	Movimiento circular uniforme.

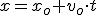
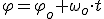
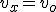
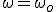
Movimiento rectilíneo uniformemente acelerado	Movimiento circular uniformemente acelerado

Ejemplo o ejercicio resuelto

Un tractor se mueve con velocidad constante de 5 m/s en línea recta.

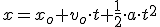
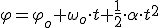
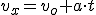
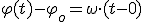
¿Qué tipo de movimiento lleva un punto de la cubierta del neumático de una de sus ruedas?
Si las ruedas traseras tienen un diámetro 1,60 metros , ¿con qué velocidad angular girarán?
¿Y las ruedas delanteras si su diámetro es de 1 metro?
Mientras las ruedas traseras dan una vuelta, ¿cuántas vueltas dan las ruedas delanteras?

Supondremos que las ruedas de nuestro tractor no patinan ya que si patinasen no podríamos resolver el problema. En este caso, para que el tractor avance, las ruedas tienen que girar y cuanto más rápido lo hagan más rápido se desplazará el tractor. Piensa por un momento en el punto del contorno de una de las ruedas que toca el suelo. Al girar hacia atrás el tractor avanza hacia delante. El espacio que recorre ese punto de la rueda es el mismo que recorre el tractor. Por lo tanto la velocidad lineal de un punto del contorno de la rueda, coincide con la velocidad del tractor. Como la velocidad del tractor es constante, la velocidad lineal de los puntos del contorno de la rueda también. Esto quiere decir que esos puntos se mueven por una circunferencia a un ritmo constante. En otras palabras, se mueven con un MCU.

Claro que si conocemos la velocidad lineal de un punto del contorno de la rueda, ya podemos junto con el radio, calcular la velocidad angular. Es lógico que la rueda delantera al ser más pequeña tenga que girar más rápido. Veamos si los cálculos nos dan la razón.

Como los radios de las ruedas traseras y delanteras son respectivamente 0,80 m y 0,50, las velocidades angulares serán:

Efectivamente la rueda delantera gira más deprisa.

Para responder al último apartado tenemos que hacer uso de la ecuación ángulo-tiempo para un MCU:

Queremos saber las vueltas que da la rueda delantera mientras da una vuelta la rueda trasera. Tenemos dos ecuaciones, una para cada rueda.

La velocidades angulares las conocemos y el ángulo recorrido por la rueda trasera también, el que corresponde a una vuelta completa, es decir, radianes. Si sustituimos estos datos tenemos un sistema de dos ecuaciones con dos incógnitas:

De la segunda ecuación podemos despejar el tiempo y sustituirlo en la primera para saber qué ángulo gira la rueda delantera:

y sustituyendo el tiempo ahora en la primera ecuación, obtenemos el ángulo descrito por la rueda trasera:

« Anterior | Siguiente »