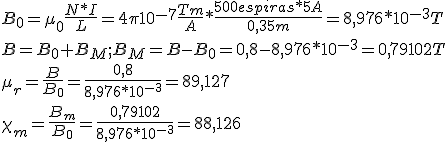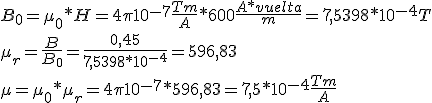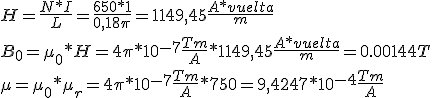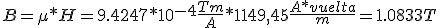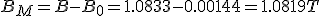Cualquiera que desde niño haya jugado con un imán habrá comprobado que estos ejercen más o menos fuerza de atracción o repulsión según su tamaño o su naturaleza. Esa fuerza puede ser medida y calculada; así como relacionada con otros parámetros. Digo esto porque ahora llegamos a la parte que más puede desagradar del tema, las fórmulas y sus resultados matemáticos. Antes de montar en cólera piensa que las matemáticas son el lenguaje con el que la Naturaleza se comunica con nosotros, tal vez no te consuele cuando un ejercicio no te salga pero sería una lástima no llegar ni siquiera a intentarlo, cuando sabemos que ese conocimiento está ahí fuera dejando que lo atrapemos. Vamos allá.

En algunas explicaciones anteriores ya hemos recurrido a algunas de estas magnitudes, como la intensidad de campo H o la permeabilidad magnética µ; en este apartado vamos a conocer algunas de ellas y cómo se relacionan y haremos algunos ejercicios prácticos.

En primer lugar tenemos que hablar de la inducción magnética, B, que no es otra cosa que la cantidad de líneas de fuerza por unidad de superficie, que en el sistema internacional se mide en Tesla (T). Si imaginamos un campo magnético, en el vacío, en el que no se produzca dispersión del flujo, tal y como resultaría el formado por un electroimán en forma de anillo la inducción magnética vendría dada por

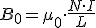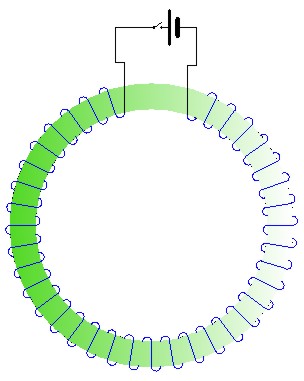
donde N sería el número de espiras de la bobina, I la intensidad de corriente que circula y L la longitud de la circunferencia media del toroide o anillo, con el que hemos formado el campo magnético, tal y como indica la imagen inferior. Así mismo, µ₀ es la permeabilidad magnética del vacío cuyo valor es 4π10^-7 (N/A²)

Imagen 9. Solenoide circular o anillo de Rowland. Fuente: Elaboración propia

Si ahora cambiáramos el anillo del solenoide por otro de otro material del que queremos conocer su inducción, observaríamos que la inducción obtenida sería

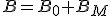donde B_M es la inducción producida por el material del anillo. Podemos deducir que para las sustancias diamagnéticas B_M tendrá valor negativo. Si ahora dividimos la expresión anterior por B₀ obtendremos

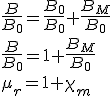siendo μ_r la permeabilidad relativa del material respecto del vacío y que es igual al cociente entre la permeabilidad absoluta del material y la permeabilidad del vacío μ_r= μ/μ₀

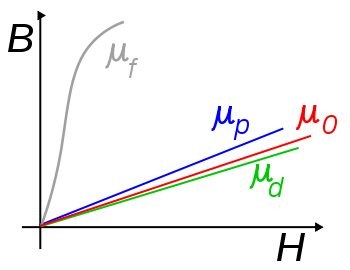
Imagen 10. Permeabilidad Magnética en función de la Inducción magnética B y la intansidad de campo H, para materiales ferromagnéticos, paramagnéticos, el vacío y diamagnéticos. Fuente: Wikipedia

 

Por otro lado χ_m es la susceptibilidad magnética que es el grado de magnetización de un material en respuesta a un campo magnético; ambas magnitudes son adimensionales.

Antes de continuar hagamos algún ejercicio.

 

En el ejercicio anterior puedes comprobar cómo se cumple la expresión μ_r=χ_m+1.

También podríamos haber calculado la permeabilidad absoluta μ=μ_r*μ_{0=89.127*4π*10^-7=1.12*10^-4 Tm/A}

Es el turno ahora de la magnetización o imanación, M y de la intensidad de campo o excitación magnética H que sí nos ha aparecido al comienzo del tema.

Hemos visto que un solenoide circular producía un campo magnético B₀ en el vacío y que si cambiábamos el anillo por otro de un material diferente, imaginemos que ferromagnético, el campo magnético obtenido era B=B₀+B_M . Podíamos suponer que ese exceso de campo magnético podía ser debido a que por la bobina del solenoide circulara una corriente adicional I_M que sumada a la inicial I generarían la inducción B. En realidad, al someter a un núcleo a la acción de un campo magnético lo que ocurre es que en dicho núcleo se producen unas corrientes que provocan la imantación del material y que reciben el nombre de corrientes amperianas.

Por lo tanto, podemos suponer que la corriente que circula por la bobina será I+I_M; así pues tendremos

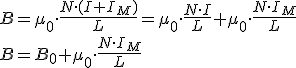A la expresión N*I_M/L es a lo que llamaremos magnetización M y a la expresión N*I/L intensidad de campo H, por lo que la expresión anterior se puede escribir como

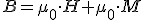Se sabe que la imanación es proporcional a la intensidad de campo, es decir M=Χ*H; por lo que podemos escribir

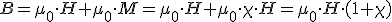La expresión (1+χ) ya nos apareció cuando hablamos de la inducción magnética, por lo que simplificando

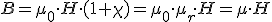de donde se deduce que μ=μ₀*μ_r, expresión que ya había aparecido con anterioridad.

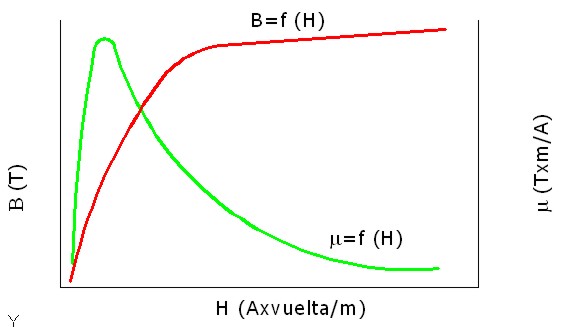
La relación entre M y H no es siempre uniforme, pues depende de factores como el tipo de material y la temperatura, por lo que en la práctica se recurre a tablas o a gráficas como la de la imagen.

Imagen 11. B/μ/H. Fuente: Elaboración propia