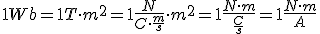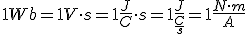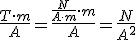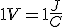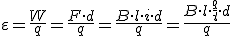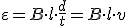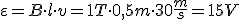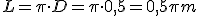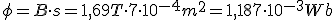4. Campos y Fuerzas Magnéticas en Conductores Eléctricos.
Seguro que si le preguntas a alguien que piense en un objeto cuando tu le digas una palabra y tú pronuncias "imán" él te responderá con cualquier cuerpo imantado de algún aparato o incluso de los que usamos para la nevera. Pero con lo que casi nadie te responderá es con "hilo de cobre" y es que, por extraño que parezca, tiene mucho que ver un conductor eléctrico con un campo magnético.
Le debemos el descubrimiento a Hans Christian Oersted, que en 1819 junto con Adré Marie Amperè, observó como una aguja imantada colocada junto a un conductor eléctrico, recorrido por una corriente, era desviada perpendicularmente; demostrando así la existencia de un campo magnético en torno a todo conductor atravesado por una corriente eléctrica.
|
|
|
Video 3. Experimento de Oersted Fuente: www.youtube.es |
La forma de este campo magnético la podemos observar si hacemos que un conductor atraviese de forma perpendicular una superficie sobre la que espolvoreamos limaduras de hierro. Cuando el conductor es recorrido por una corriente en el sentido que indica la flecha, las limaduras se reorientarán en círculos concéntricos y el sentido de estos círculos, que es el sentido de las líneas de fuerza, lo podemos obtener si figuradamente nuestra mano derecha agarra el conductor y nuestro pulgar señala el sentido de la corriente eléctrica, el resto de nuestros dedos señalará el sentido del campo magnético circular originado en el conductor.
 |
 |
|
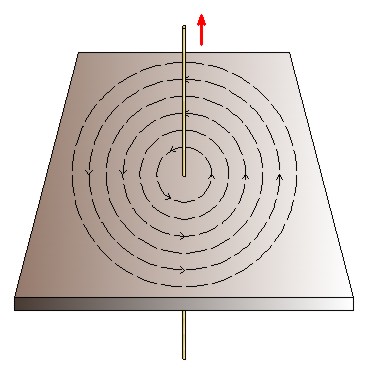
Imagen 19. Campo circular producido por un conductor Fuente: Elaboración propia |
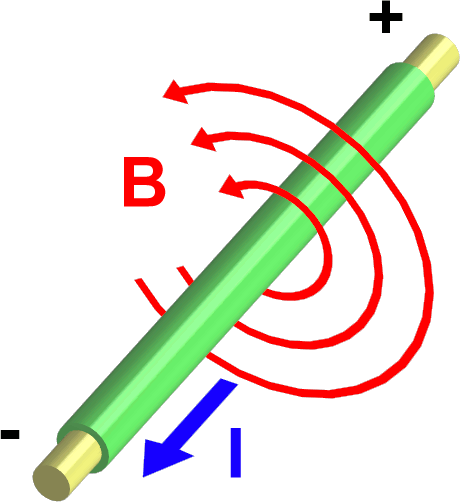
Imagen 20. Dirección del campo en un conductor Fuente: Wikipedia |
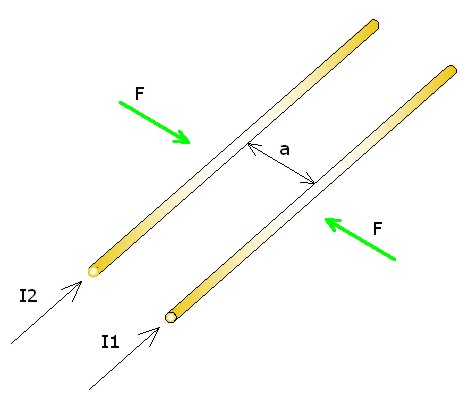
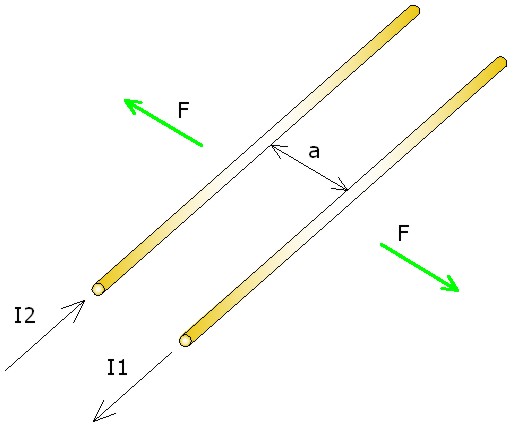
Teniendo claro ya que una corriente eléctrica produce un campo magnético, vamos a usar dos conductores de longitud L, recorridos por corrientes I1 e I2, separados una distancia a, para observar los efectos que en ellos producen los campos magnéticos.
Así observaremos que si las corrientes son del mismo sentido, los conductores se atraen y si los sentidos son diferentes se repelen
 |
|
|
Imagen 21. Conductores atrayéndose por la acción de un campo Fuente: Elaboración propia |
Imagen 22. Conductores separándose por la acción de un campo Fuente: Elaboración propia |
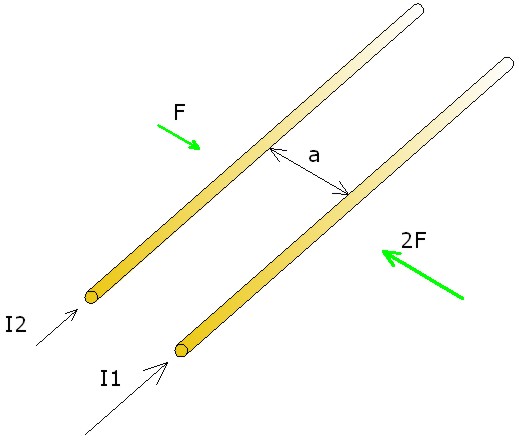
Si la intensidad en uno de los conductores aumenta dos o tres veces, también lo hace la fuerza en él generada.
 |
|
Imagen 23. Variación de la fuerza al variar la intensidad Fuente: Elaboración propia |
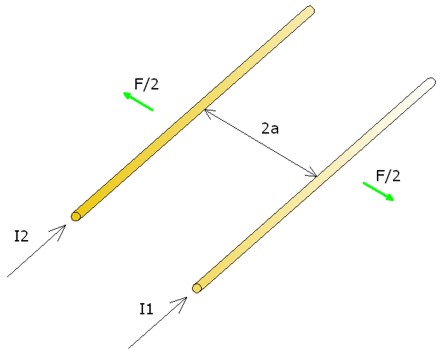
Y por último, si la distancia entre los conductores disminuye, la fuerza aumenta; y si la distancia aumenta, la fuerza disminuye.
 |
|
Imagen 24. Variación de la fuerza al variar la separación Fuente: Elaboración propia |
Todos estos experimentos, y sus conclusiones, nos permiten obtener una expresión que relaciona la fuerza por unidad de longitud con que el conductor 1 atrae al 2
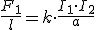 |
La expresión anterior se puede escribir de otra manera gracias a la ley de Biot-Savart, que determina la relación existente entre una corriente rectilínea y el campo magnético creado por ella a una distancia a
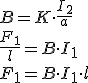 |
donde B es la inducción magnética ya conocida por nosotros y la constante K es igual a μ0/4π, siendo μ0 la permeabilidad magnética del vacío. Por otro lado, se ha observado en los experimentos que la fuerza generada es perpendicular a la circulación de la corriente y el campo magnético por ésta generado también lo es y a su vez perpendicular a la fuerza.
No te preocupes que vamos a recurrir a una regla nemotécnica para poder recordar tanta perpendicularidad y así poder identificar el vector de cada magnitud, eso sí, tienes que conocer el nombre de los dedos de tu mano.
|
|
|
Imagen 25. Regla de la mano izquierda Fuente: Elaboración propia |
El dedo pulgar indicará la dirección de la fuerza F, el dedo índice el campo magnético B y el corazón el sentido de la corriente I. Familiarízate con la posición de los dedos, todos ellos forman 900 entre sí y di movimiento, campo, corriente con suerte ya no lo olvidarás (mocaco).
Si profundizamos en la expresión de F1 de más arriba, generalizándola para cualquier conductor, se producirá una fuerza F. En él, la corriente I no será más que un flujo de cargas, es decir I=q/t, y si sustituimos
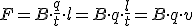 |
considerando la unidad de carga eléctrica q, y teniendo en cuenta que la carga se desplaza por el conductor la distancia l; v=l/t será la velocidad de la carga, tal y como se refleja en la expresión. De forma vectorial sería.
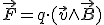 |
Por último señalar que siempre el ángulo formado por el conductor y el campo es de 900 ; si ese no fuera el caso, entonces la expresión de F se vería afectada del seno del ángulo y observando que si el conductor es paralelo al campo, entonces no se producirá fuerza, pues sen 900 = 0
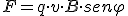 |
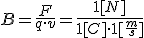 |
el Tesla será la inducción de un campo magnético tal que una carga de un coulombio desplazándose perpendicularmente dentro del campo a la velocidad de 1 m/s, experimenta una fuerza de un newton.
Cuando en el apartado 2.2 definimos la inducción magnética, dijimos que era la cantidad de líneas de fuerza por unidad de superficie, pero si de lo que se trata es de conocer el número total de líneas de fuerza que atraviesan un cuerpo dentro de un campo magnético, es decir el flujo magnético Φ, entonces
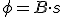 |
El flujo magnético se mide en webers Wb; 1Wb=1Tm2